一、实验目的：

  1. 掌握回溯法算法设计思想。
  2. 掌握地图填色问题的回溯法解法。

二、内容：

背景知识：

为地图或其他由不同区域组成的图形着色时，相邻国家/地区不能使用相同的颜色。 我们可能还想使用尽可能少的不同颜色进行填涂。一些简单的“地图”（例如棋盘）仅需要两种颜色（黑白），但是大多数复杂的地图需要更多颜色。

每张地图包含四个相互连接的国家时，它们至少需要四种颜色。1852年，植物学专业的学生弗朗西斯·古思里（Francis Guthrie）于1852年首次提出“四色问题”。他观察到四种颜色似乎足以满足他尝试的任何地图填色问题，但他无法找到适用于所有地图的证明。这个问题被称为四色问题。长期以来，数学家无法证明四种颜色就够了，或者无法找到需要四种以上颜色的地图。直到1976年德国数学家沃尔夫冈·哈肯（Wolfgang Haken）（生于1928年）和肯尼斯·阿佩尔（Kenneth Appel，1932年-2013年）使用计算机证明了四色定理，他们将无数种可能的地图缩减为1936种特殊情况，每种情况都由一台计算机进行了总计超过1000个小时的检查。

他们因此工作获得了美国数学学会富尔克森奖。在1990年，哈肯（Haken）成为伊利诺伊大学（University of Illinois）高级研究中心的成员，他现在是该大学的名誉教授。

四色定理是第一个使用计算机证明的著名数学定理，此后变得越来越普遍，争议也越来越小 更快的计算机和更高效的算法意味着今天您可以在几个小时内在笔记本电脑上证明四种颜色定理。

问题描述：

我们可以将地图转换为平面图，每个地区变成一个节点，相邻地区用边连接，我们要为这个图形的顶点着色，并且两个顶点通过边连接时必须具有不同的颜色。附件是给出的地图数据，请针对三个地图数据尝试分别使用5个（le450_5a），15个（le450_15b），25个（le450_25a）颜色为地图着色。

三、实验要求

1、对下面这个小规模数据，利用四色填色测试算法的正确性；

2、对附件中给定的地图数据填涂；

3、随机产生不同规模的图，分析算法效率与图规模的关系（四色）。

四、算法原理描述

1、朴素回溯

1）算法描述:每次对当前需要染色的节点选择一种它可以使用的颜色进行染色，然后进行下一个节点的染色，直到所有节点染完颜色，染色方案的数量就会加一。然后回到上一个节点继续枚举它可以使用的颜色进行染色。直到将所有的染色方案找出为止。

如下图，如果只有四个节点，四种颜色，当左侧的图染完颜色之后就将3号点和4号点的颜色删除，往下枚举3号点可以使用的颜色，接着对该图进行染色，就可以得到右侧另外一种染色方案，这样枚举下去，直到找出所有方案。

2）伪代码描述：

1
2
3
4
5
6
7
8
9
10
dfs(t)
	if t > point_num then
		ans_num ++ 
		return
		
	for i from 1 to color_num
		if check(t, i) then 
			color[t] = i
			dfs(t + 1)
			color[t] = 0

3）算法时间复杂度：设节点数为n， 颜色数为c，每个节点都有c种颜色可以选择，那么解空间就有$cn$ 个节点，而朴素回溯是枚举每一种方案所以时间复杂度为$O(Cn)$

时间复杂度为指数级，需要采用合适的剪枝策略进行优化

2、剪枝策略

1.优化搜索顺序：在染色的过程中，按照不同的顺序对节点进行染色其对应的搜索树的各个层次，各个分支之间的顺序不是固定的，不同的搜索顺序会产生不同的搜索树形态，它们的规模大小也相差甚远。

如下图中的两棵搜索树，它们的叶子节点对应的是相同解决方案，左图的搜索树一开始就选分支数量较多的节点搜索，有可能直到搜索深度较深的时候才会将不合法的的方案排除，而右图中的搜索树则选择从分支数量较少的节点开始搜索，有可能在搜索深度较浅的时候就就不合法的方案排除。所以在搜索的时候应该尽量选择分支较少的搜索顺序进行搜索（即DH准则）和优先搜索分支较少的节点（即MRV准则）

在刚开始染色的时候选择度数最大的节点对其周围的节点产生的约束条件最强，使得最多的节点减少一种可使用的颜色，使得整棵搜索树的分支较少，所以第一个染色的节点应选择度数最大的节点（即DH准则）。

如下图，如果优先对SA节点染色，那么其他的节点可用的颜色就全部减少一种，其对应搜索树的宽度大大减小。

在搜索过程中，优先选择可填颜色最少的节点（MRV准则），也即优先选择分支最少的节点可以减少搜索次数，尽早排除不合法的方案。

如下图，染色顺序的第三步中未染色的节点分别有1、2、3、3种颜色可以使用，如果选择剩下三种颜色的节点先染色的话，那么对应的就会产生三条分支，而选择剩下一种颜色的节点进行染色的话对应就只产生一条分支，大大减少了搜索次数。

3.可行性剪枝:在染色的过程中，及时对当前的状态进行检查，如果发现当前分支已经完成所有节点的染色，那么就执行回溯。

如下图，如果可以使用的颜色只有四种，左图中间节点的周围节点都已经染上颜色，那么就会发现中间这个节点没有剩余的颜色可填，那么就执行回溯，回到4号节点使用下一种颜色，那么中间节点就有可以使用的颜色，并完成当前整个图的染色。

上述过程只是检查当前节点的染色状态并执行剪枝，而向前探查则在当前节点染色完毕后对其相邻节点进行检查，如果其相邻节点并未染色并且没有剩余颜色可以使用那么当前状态不合法，执行回溯。使用向前探查的方法可以减小搜索过程中搜索不合法分支的深度。

4．排除等效冗余:在搜索过程中，如果我们能够判定从搜索树的当前节点上沿着某几条不同分支到达的子树是等效的，那么只需要对其中的一条分支执行搜索。

对应的，在染色的过程当中，如果当前需要染色的点有 x 种从未被其他点使用过的颜色可以使用，则这 x 种颜色可以视为等价的颜色，直接使用其中一种颜色后，计算其他点的染色方案数，令方案数乘以 x 即可。

例如，对于下面的图，假设有四种颜色可以使用，那么利用排列组合的原理，可以计算出下图有 $4！= 24$ 种染色方案

类似的，对于下图，假设有三种颜色可以使用，那么下图将会有$2！+2！+2！+3！= 12$种染色方案

由于n种颜色对应的全排列有 $n!$ 种，所以该方法可以极大的提高搜索效率。

2）伪代码描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
dfs(pt, level)
`    `if(level > point\_num) return 1
`    `for(int i = 1; i <= color\_num; i ++ )
`        `if 颜色i不应使用 then continue
`        `color[pt] = i   //染色
`		`对本次染色点的邻点进行操作并寻找下一节点染色
`        `if 该颜色第一次使用 then
`            `tmp\_unuse = unuse
`            `unuse -- , used[i] ++ 
`            `ans += dfs(nextpt, level + 1) \* tmp\_unuse
`            `unuse ++ , used[i] -- 
`       `else if 该颜色不是第一次使用 then
`			`used[i] ++ 
`			`ans += dfs(nextpt, level + 1)
`			`used[i] -- 
`        `回溯，恢复原有状态
`	`return ans

五、效率分析

注：下面的列表中Prune代表没有使用等效冗余的剪枝算法，而MathP则代表使用了排除等效冗余的剪枝算法

1.附件数据分析

小规模 五色 十六色 二十五色
方案数量(MathP) 480 3840 2.09E+13 1.55E+25
耗时/ms 0.052352 202 2.721264 2.944414
方案数量(Prune) 480 3840 1.00E+10 1.00E+10
耗时/ms 0.057918 3806 145408 90217
耗时比 1.106319 18.8 53433.99 30640.05

由于$16! = 20922789888000$，$25! = 15511210043330985984000000$

所以使用排除等效冗余的剪枝算只需要搜索出一组解，即可等效出其颜色数量对应的阶乘组解，因此十六色和二十五色对应的数据集只需要几毫秒的时间就搜索出十几位数大小的染色方案数量。而当解空间较小时，如上表中的小规模数据，排除等效冗余的算法尽管比没有排除的算法快，但优势体现得不明显，图越稠密，颜色数量越多，其优势

2.随机图效率分析

1）点数固定为二十个点，边数由稀疏增加到稠密

点数 边数 颜色数 Prune时间(ms) MathP时间（ms） 时间比值取对数
20 20 4 42482 6496 0.815558938
20 40 4 76 11 0.839420907
20 60 5 120 6 1.301029996
20 80 6 955 10 1.980003372
20 100 7 6769 9 2.876282005
20 120 10 49362 4 4.091332756
20 140 12 88909.66339 4.270977 4.318421733
20 160 13 115045.9889 0.039866 6.460268819
20 180 16 295174.936 0.026392 7.048607175

上表中对应的额染色方案数量列表

点数 边数 Prune MathP
20 20 3501133308 3501133308
20 40 6336288 6336288
20 60 11043720 11043720
20 80 83416320 83416320
20 100 629712720 629712720
20 120 10000000000 2.85626E+11
20 140 9999999996 2.15129E+13
20 160 9999999997 1.09596E+12
20 180 10000000000 4.81224E+14

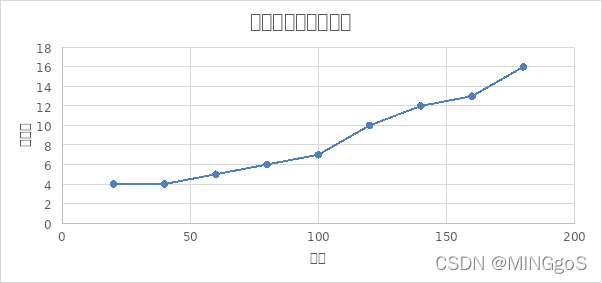
由上图可以看出，点的数量一定时，图越稠密，使用的测试数据需要使用的颜色数量越多

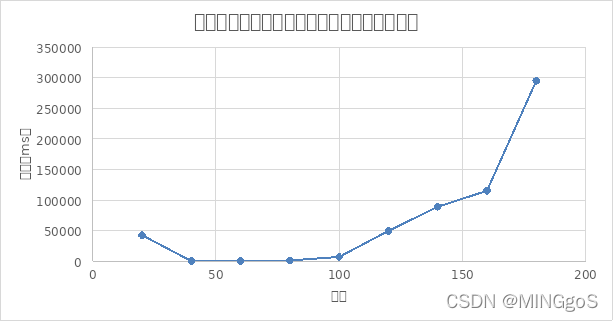
由图像可得，当图极其稀疏时，随着边数的增加，算法运行的时间会逐步减少，而当图逐渐稠密时，算法运行的时间也逐渐开始变长

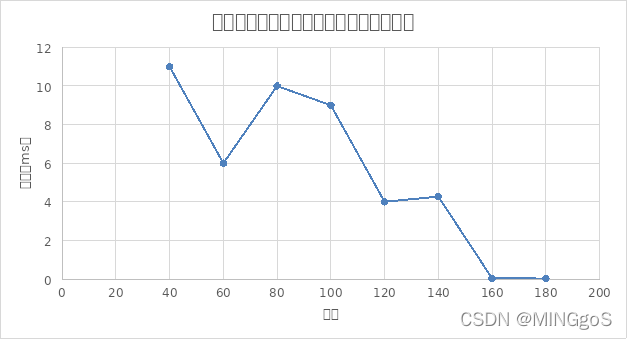
(注：边数为20时，使用该算法得到的运行时间为6496ms，与其他边数差值过大，故未在图中画出)

由图像可得，当图越稠密，颜色数量越多，排除等效冗余的算法效率也会相应的提高，算法总体运行时间的趋势是往下降的，中间的运行时间有部分往上升的，这主要取决于点与点之间的约束关系，即图本身的复杂程度

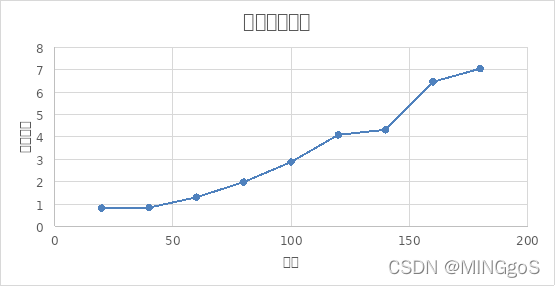
上图为没有使用等效冗余的算法运行时间与使用等效冗余的算法运行时间的比值取对数的图，可以看出比值的对数与边数呈现正相关的关系，120条边之后曾长速度略有下降，主要是因为没有使用等效冗余的算法搜索完100亿组解之后就退出不再进行搜索

2）边数固定为四十五条边，逐渐增加点数

点数 边数 颜色数 Prune时间(ms) MathP时间（ms） 时间比值取对数
10 45 10 79.89145 0.003464 4.36292242
15 45 5 7.442274 0.351904 1.325281452
20 45 5 21022.43152 727.384756 1.460918751
25 45 4 49676.92409 7451.619834 0.823904007

上表中对应的额染色方案数量列表

点数 边数 Prune MathP
10 45 3628800 3628800
15 45 384960 384960
20 45 1378805760 1378805760
25 45 2233151424 2233151424

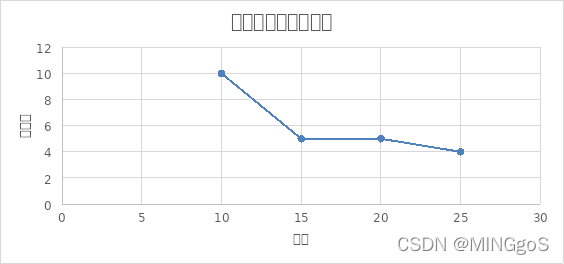
由上图可得边数固定时，点数越多，即图越稀疏，使用的测试数据需要用到的颜色数量呈现减少的趋势

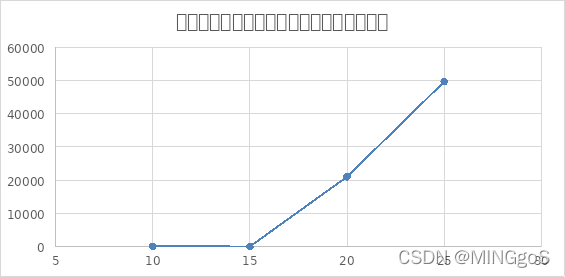
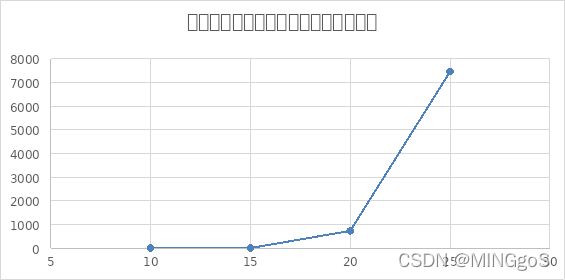
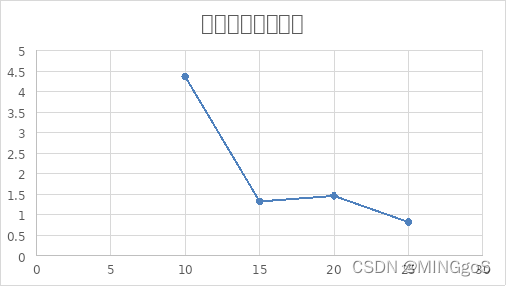
综合上面三个图像可以得出，无论是排除等效冗余还是不排除，在边数固定的情况下，点数越多，即图越稀疏，需要用到的颜色数量越少，算法运行需要的时间越长，而且排除等效冗余的效率也开始逐渐下降，与不排除等效冗余的运行时间比值呈现下降的趋势。

以上数据分析只能说明使用的测试数据情况如此，不能代表所有的随机图都是这样，要得出所有图自身的边数点数颜色数与算法效率之间的关系还要取决于图本身的复杂程度，即图本身点与点之间的约束关系

六、实验心得

  1. 回溯法是将所有的解（问题的解空间）按照一定结构排列，再进行搜索的一种解决问题的方法，其本质就是枚举，时间复杂指数级的，当问题的规模较大时，使用朴素回溯就不太合适了

  2. 剪枝算法对于提高回溯搜索的效率具有重要的意义，一个好的剪枝算法可以极大地提高回溯的搜索效率

  3. 不同的问题有不同的剪枝策略，需要具体问题具体分析，结合实际做出不同的剪枝策略