算法设计实验四
一、实验目的:
- 掌握动态规划算法设计思想。
- 掌握流水线问题的动态规划解法。
二、内容:
汽车厂有两条流水线,每条流水线有n个处理环节(station): S1,1,…,S1,n 和 S2,1,…,S2,n,其中下标的第一个字母表示流水线编号(流水线1和流水线2)。其中S1, j 和 S2, j 完成相同的功能,但是花费的时间不同,分别是a1, j , a2, j 。两条流水线的输入时间分别为e1 和 e2, 输出时间是x1 和 x2。
每个安装步骤完成后,有两个选择:
1)停在同一条安装线上,没有转移代价;
2)转到另一条安装线上,转移代价: Si,j 的代价是ti,j , j = 1,…,n - 1
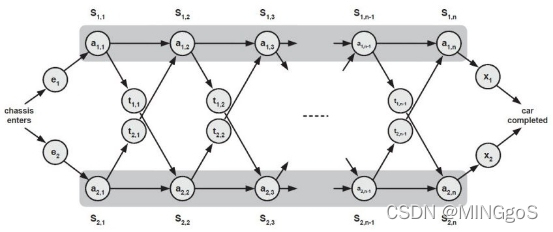
问题: 如何选择安装线1和安装线2的节点组合,从而最小化安装一台车的总时间?
三、实验要求
1、给出解决问题的动态规划方程;
2、随机产生S2, j 、ti,j的值,对小数据模型利用蛮力法测试算法的正确性;
3、随机产生S2, j 、ti,j的值,对不同数据规模(n的值)测试算法效率,并与理论效率进行比对,请提供能处理的数据最大规模,注意要在有限时间内处理完;
4、该算法是否有效率提高的空间?包括空间效率和时间效率。
四、算法原理描述
1、回溯剪枝(暴力枚举)
1)算法描述:利用回溯法遍历计算所有解对应的代价,找出其中的最小值。
搜索树定义:
解空间:$n$个变量,每个变量有两种取值所以总共有$O(2^n)$ 种解
节点定义:$(x1,x2,…,x7)$,xi取值范围{0,1}$
状态树的构造:在两条流水线中选择其中一条以进入下一层的搜索。
树最多有$n + 1$层(根是第0层)
每个叶子节点就是一种解,遍历所有叶子节点找出代价最小的解
如下图,四个叶子节点中的最小值为12,枚举这个四个叶子节点,找出12这个最小值。

在进行回溯的过程中还可以进行一些比较简单的剪枝。在进行搜索的过程中,如果来到当前节点所需要的代价已经大于或等于当前记录下来的最小代价时,由于到下一个节点进行处理的代价是正值,那么总的代价也会呈现递增的趋势,这个时候就直接回溯。
如下图,当搜索到③号节点时,当前需要的代价为14,已经大于当前搜索出来的最小值12,那么就直接回溯。

2)伪代码描述:

3)算法时间复杂度:设每条流水线有n个处理节点,每个节点都有两个方向可以选择,那么解空间就有$2^n$ 个节点,枚举每一种方案的时间复杂度为$O(2^n)$
2、动态规划
1)状态表示:
流水线问题要求的是总的耗时最短的路线组合,我们可以将$f_i[j]$设为最快通过处理站 $S_{i,j}$的时间,即$f_i[j]$为所有到达站点 $S_{i,j}$的路线总时间中的最小值。设$f$为通过整个流水线的最短时间
2)边界条件
$j=1, i=1, 2$ 时,底盘送入流水线,第一步的时间为输入时间加上工序时间,故边界条件为:
$f_1[1] = e_1+a_{1,1}$
$f_2[1] = e_2+ a_{2,1}$


3)阶段划分
观察下面两张图可以发现,要到达 $S_{1,2}$的最短时间 $f_{1,2}$由需要从 $S_{1,1}$或者 $S_{2,1}$出发
要到达 $S_{1,3}$的最短时间 $f_{1,3}$由需要从 $S_{1,2}$或者 $S_{2,2}$出发
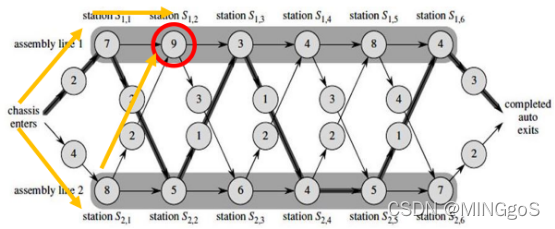
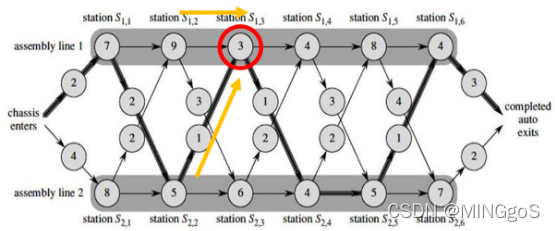
可以看出问题fi[j]是在上一个阶段的基础上构成,所以可以推测该问题具有最优子结构
证明:
假设$fi[j]$为最优,而其子问题 $h1[j - 1]$不是最优,那么存在子问题的最短时间 $f1_j - 1 < h1[j - 1]$ 为最优,交换$ f1[j - 1]与 h1[j - 1]$得出 $f’i[j] < fi[j]$为最优,那么 $fi[j] $不是最优解,矛盾。
该问题符合最优子结构的性质,同理可证其他情况。证毕。

所以我们可以将阶段划分如下: $f1j - 1, f2j - 1$是前一阶段
求 $f1j、 f2$j为后一阶段
4)状态计算
由阶段划分的分析,我们不难发现到达 $S1,j$的路线可以分为从站点 $S1,j-1$而来和从站点 $S2,j-1$而来,又由于该问题具有最优子结构,那么求$f1[j]$可以转化为求$f1[j-1]$和$f2j-1+t2[j-1]$二者之间的最小值,得出最小值后再加上站点 $S1,j$需要的时间 $a1 j$,同理可求$f2[j]$


通过整个流水线的最短时间$f_*$则由$f1[n]+x1$ 和 $f2[n]+x2$ 二者之间的较小值得出

至此,我们可以写出状态转移方程为


$f_*=min(f1[n]+x1,f2[n]+x2)$
2)伪代码描述
求解最短时间
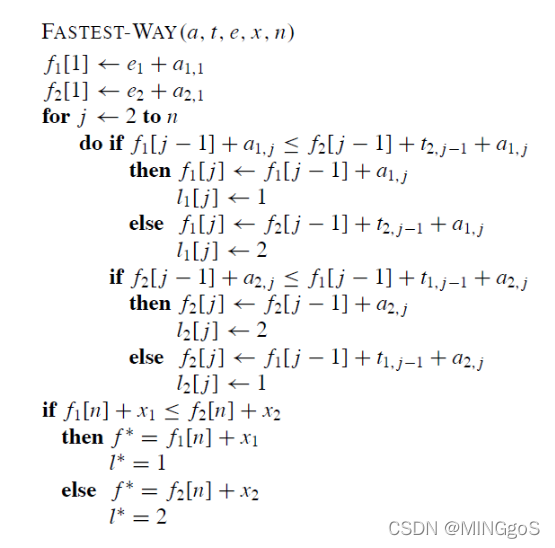
3)算法复杂度分析:
时间复杂度:每次计算需要计算两个站点,每个站点计算前面两个站点到本站点时间的最小值,可以得出时间复杂度为$O(n)$
空间复杂度:$O(n)$,但存储信息为中间过程的时间最小值,每个站点的处理时间,每个站点的转移代价,流水线转移路径,常数较大,可进一步优化
4)优化方案
由于每次的状态计算只与上一阶段的状态有关,所以可以不记录中间结果,只记录流水线转移路径, 每个站点的处理时间,每个站点的转移代价都可以不存储。
在计算机中,一个char类型字符占用一个字节的存储空间,而一个int类型占用4个字节,所以使用char类型数组代替int类型数组存储路径可以提高测试的最大规模。
在Windows系统下,栈是向低地址扩展的数据结构,是一块连续的内存的区域。栈的大小受限于编译器。如果申请的空间超过栈的剩余空间时,将提示overflow。因此,能从栈获得的空间较小。
而堆是向高地址扩展的数据结构,是不连续的内存区域。系统是用链表来存储的空闲内存地址的。堆的大小受限于计算机系统中有效的虚拟内存。因此堆能获得的空间比栈的空间要大。
将数组开辟到堆区可以进一步提高测试数据的最大规模。
状态转移方程:
$h1= f1 ,h2= f2$
$f1 = e1+a_{1,1}, if - j=1$
$f1 = min(h1, h2+t2,j -1)+a_{1,j} , if - j≥2$
$f2 = e2+a_{2,1}, if - j=1$
$f2 = min(h2, h1+t1,j -1)+a_{2,j }, if - j≥2$
$f_*=min(f1+x1,f2+x2)$
伪代码描述

5)路径输出函数
思路:逆序输出后面的节点是由前面哪一个节点转移而来

时间复杂度:$O(n)$,空间复杂度:$O(n)$
五、效率分析(时间单位:us)
O(n)复杂度时间理论值推导
$tl=n1 * t$, t1表示规模为n1的数据用时
$t2=n2 * t$ t2表示规模为n2的数据用时
$t2=(n2/n1) * t1$
记录了所有中间结果以及转移代价和处理时间的算法效率:
时间单位:us
| Input | dp1 | 理论值 |
|---|---|---|
| 10000000 | 57065.9 | 56099.17 |
| 20000000 | 112016 | 112198.3 |
| 30000000 | 168418 | 168297.5 |
| 40000000 | 225884 | 224396.7 |
| 50000000 | 281895 | 280495.8 |
| 60000000 | 336595 | 336595 |
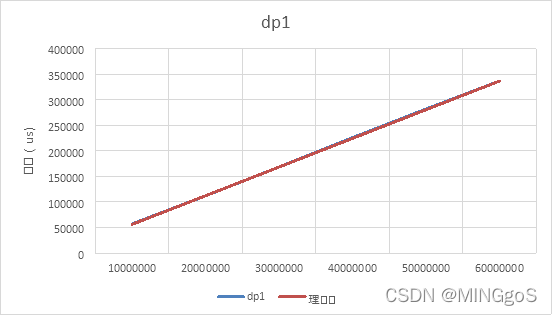
能达到的最大测试规模为六千万
观察图表可得,实测效率曲线与理论效率曲线拟合较好,实测效率满足理论分析,实际时间复杂度为$O(n)$
不记录最小处理时间中间结果但记录各种代价以及路径的时间效率:
时间单位:us
| Input | dp2 | 理论值 |
|---|---|---|
| 10000000 | 44304.3 | 44142.38 |
| 20000000 | 88556.1 | 88284.75 |
| 30000000 | 133542 | 132427.1 |
| 40000000 | 177171 | 176569.5 |
| 50000000 | 221502 | 220711.9 |
| 60000000 | 264927 | 264854.3 |
| 70000000 | 308989 | 308996.6 |
| 80000000 | 353139 | 353139 |
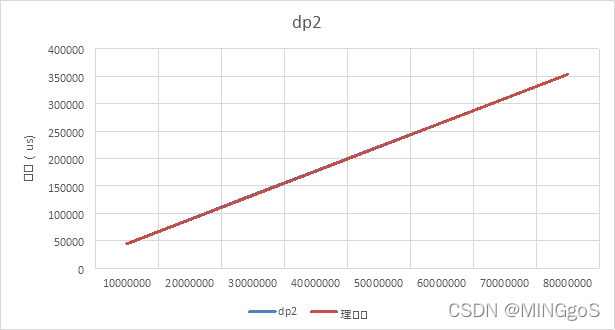
能达到的最大测试规模为八千万
观察图表可得,实测效率曲线与理论效率曲线拟合较好,实测效率满足理论分析,实际时间复杂度为$O(n)$
二者六千万规模部分的对比:

比值的平均值为1.27204
记录最小处理时间中间结果的算法时间复杂度的常数较大,这因为访问数组的代价要比访问单个变量的代价开销要大
只记录路径的算法时间效率
| Input | dp2 | 理论值 | 随机数时间 | 差值 | 理论值2 |
|---|---|---|---|---|---|
| 30000000 | 1.59E+06 | 1578925 | 1.47E+06 | 1.22E+05 | 109804.8 |
| 60000000 | 3.16E+06 | 3157850 | 2.94E+06 | 2.23E+05 | 219124.7 |
| 90000000 | 4.74E+06 | 4736775 | 4.41E+06 | 3.33E+05 | 328929.4 |
| 1.2E+08 | 6.33E+06 | 6315700 | 5.87E+06 | 4.54E+05 | 438209.8 |
| 1.5E+08 | 7.90E+06 | 7894625 | 7.34E+06 | 5.61E+05 | 547602.1 |
| 1.8E+08 | 9.49E+06 | 9473550 | 8.83E+06 | 6.61E+05 | 658633.1 |
| 2.1E+08 | 1.11E+07 | 11052475 | 1.03E+07 | 7.65E+05 | 768634 |
| 2.4E+08 | 1.26E+07 | 12631400 | 1.18E+07 | 8.77E+05 | 876800 |
由于在dp函数内部生成随机数,所以总的时间也包含了随机数生成的时间。记录同等规模的随机数所需的时间与总的时间作差得出实际在计算所用的时间。
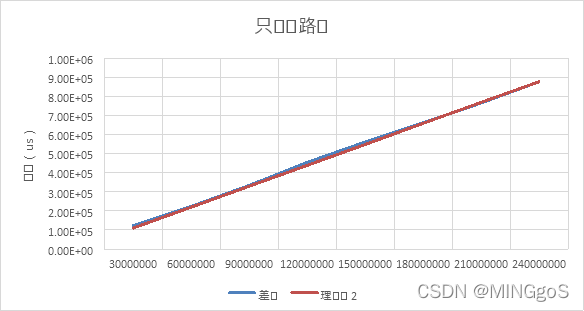
观察图表可得,实测效率曲线与理论效率曲线拟合较好,实测效率满足理论分析,实际时间复杂度为$O(n)$
测试数据的最大规模
Int类型数组记录路径(只记录路径)
最大数据规模:$2.4E+08$(两亿四千万)
处理时间:8.77E+05(us)(0.877秒)
Char类型数组记录路径(只记录路径)
最大数据规模:$9.9E+08$(九亿九千万)
处理时间:6.07E+06(us)(6.07秒)
分析:char类型占一个字节,而int类型占四个字节,所以数据规模大概为int类型的四倍。使用char类型变量赋值时,会发生隐式类型转换这部分的开销较大,所以处理时间比int类型的处理时间的四倍要高
将char类型数据开辟到堆区(只记录路径)
最大数据规模:$21.4E+08$(二十一亿四千万)
处理时间:1.54E+07(us)(15.4秒)
分析:堆区处理时间/栈区处理时间 = 1.54E+07 / 6.07E+06 ≈ 2.54
堆区数据规模/栈区数据规模 = 21.4E+08 / 9.9E+08 ≈ 2.16
堆区处理速度:堆区数据规模/堆区处理时间=9.9/6.07≈1.3896(亿/s)
栈区处理速度:栈区数据规模/栈区处理时间=21.4/15.4≈ 1.6309(亿/s)
可见堆区的处理速度要慢于栈区的处理速度
堆区内存使用的是链表存储,而栈区内存使用连续的空间存储,所以访问堆区的内存要慢于访问栈区的内存,但优点在于可利用的空间更大。
六、实验心得
-
DP问题的难点主要在于找出状态转移方程。
-
很多算法都是问题的可划分性以及子问题之间的相似性来进行归纳,降低求解的复杂度。动态规划也不例外。
-
动态规划的艺术在于状态设计和子结构的发掘,如何把问题形式化为状态空间,进一步抽象出DP的状态表示和阶段划分,是一件值得探究的事。