算法设计实验五
一、实验目的:
- 掌握图的连通性。
- 掌握并查集的基本原理和应用。
二、内容:
1. 桥的定义
在图论中,一条边被称为“桥”代表这条边一旦被删除,这张图的连通块数量会增加。等价地说,一条边是一座桥当且仅当这条边不在任何环上。一张图可以有零或多座桥。
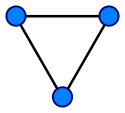
图 1 没有桥的无向连通图
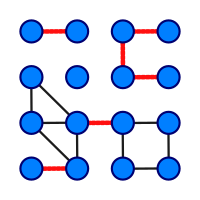
图 2 这是有16个顶点和6个桥的图(桥以红色线段标示)
2. 求解问题
找出一个无向图中所有的桥。
3. 算法
(1)基准算法
1 |
|
(2)应用并查集设计一个比基准算法更高效的算法。不要使用Tarjan算法,如果使用Tarjan算法,仍然需要利用并查集设计一个比基准算法更高效的算法。
三、实验要求
- 实现上述基准算法。
- 设计的高效算法中必须使用并查集,如有需要,可以配合使用其他任何数据结构。
- 用图2的例子验证算法正确性。
- 使用文件 mediumG.txt和largeG.txt 中的无向图测试基准算法和高效算法的性能,记录两个算法的运行时间。
- 设计的高效算法的运行时间作为评分标准之一。
- 提交程序源代码。
- 实验报告中要详细描述算法设计的思想,核心步骤,使用的数据结构。
四、算法原理描述
1、基准算法
使用的数据结构:邻接表。
由于实际应用中大多为稀疏图,使用邻接矩阵则会有大量的空白数据,将造成较大的浪费,会导致dfs遍历的无效次数增多
基准法1
1)算法描述:首先用dfs 或者bfs 计算出图中共有几个连通块,如果当前搜索的连通块中节点都已经被被访问过,而整个图的节点还没有被完成访问过,则连通块的数量加一,并进入下一个连通块进行搜索,枚举完所有节点以计算出有几个连通块。
如下图,当访问完A点所在的连通块中所有的点,还有其他灰色的点没有被访问过,那么连通块的数量加一,并开始访问其他点所在的连通块,以此计算出这种图共有4个连通块。

计算出图中总共有几个连通块之后,开始计算图中共有多少条桥。一条边被称为“桥”代表这条边一旦被删除,这张图的连通块数量会增加。因此,只需要将图中任意一条边删除,再计算出图中共有几个连通块,与删除边之前的连通块数量作比较,如果连通块的数量增加,那么,被删除的这条边就是桥。
如下图,原本A,B两点之间连接有一条边,使得A,B两点处于同一个连通块之中,而删去AB这条边后可以发现此时,A,B两点位于不同的连通块之中,连通块的数量从4个变成了5个,说明AB这条边是桥。

按照这种思路依次枚举图中所有的边,就可以找出所有的桥。
2)伪代码描述:

CountBlock( )函数用于在开始搜索之前计算不删除边时,这个图有几个连通块

3)算法时间复杂度: n为点数,m为边数,每次计算连通块的数量需要枚举图中的所有节点,单次计算连通块的数量的时间复杂度为 $O(n + m)$,共有m条边需要计算m次,因此总的时间复杂度为 $O(m n + m^2)$
基准法2
1)算法描述: 从桥的定义出发,一条边是一座桥当且仅当这条边不在任何环上。对于图中的任意一条边,如果删去这条边,而这条边对应的两个点不再连通的话,说明除了这条边,没有其他路径可以使得这两个点连通,那么这条被删掉的边就是桥。而如果两点之间依旧连通的话,说明这条边处在一个环里面,存在其他路径使得这两个点连通,那么这条被删掉的边就不是桥。
两点之间的连通性可以通过对其中一个点进行一次深度优先搜索进行判断,如果在深度优先搜索的过程访问到了另外一个节点,那么就说明两点是连通的,停止搜索。
如下图,A,B两点之间原本是相互连通的,删去AB这条边,对A进行深度优先搜索,搜索结束时,依旧没有访问过B点,说明除了AB这条边之外,A点和B点再也没有其他连通的路径,那么AB这条边就是桥,依次枚举图中的每一条边,即可找出所有的桥。

2)伪代码描述:


3)算法时间复杂度: n为点数,m为边数,每次查看两点的连通性在最坏情况下要枚举n个点,时间复杂度为$O(n + m)$,共有m条边需要计算m次,总的时间复杂度为$O(m n + m^2)$
2、优化
在图论中,无向图 G 的生成树(英语:Spanning Tree)是具有 G 的全部顶点,但边数最少的连通子图。换句话说,树会使得所有的顶点连通,并且不会形成环。那么桥一定会出现在树边上,而不会出现在非树边上。
如下图,对于子图A 和 子图B 他们之间有唯一的一条边使得他们之间保持连通,那么在这个图的生成树一定会包含这条边,否则子图A子图B之间不连通。

而对于下图,假设黄色的边为树边,而灰色的边为非树边,那么当删去灰色边时,连通块的数量不会增加,说明这条灰色的边不是桥,对于一张图中的生成树来说,它的树边已经能保证所有的节点之间相互连通,而这个时候再往树中添加任意一条非树边就一定会和其他的树边形成环,非树边一定不是桥。

这个时候就可以使用基准法来枚举这些树边以找出所有的桥。需要枚举的边从整张图的m条边降低为生成树的$n – 1$ 条边,而对于非连通图来说,需要枚举的就是生成森林的树边。
如下左图,对它进行生成树的生成,就会得到右图中的森林,对于森林中树的树边进行枚举即可

对于稠密图来说,枚举树边会使效率得到大幅度的提升。
2)伪代码描述:
生成生成树的伪代码:


使用生成树的树边进行枚举:

3)算法时间复杂度: n为点数,m为边数,一棵树有n – 1 条边,基准法原来需要枚举m条边,现在只需要枚举树边,时间复杂度从
$O(m n + m^2)$降低为$O(m n + n^2)$
3、并查集
并查集是一种树形的数据结构,用于处理一些不交集(一系列没有重复元素的集合)的合并及查询问题。
并查集支持如下操作:
查询:查询某个元素属于哪个集合,通常是返回集合内的一个“代表元素”。这个操作是为了判断两个元素是否在同一个集合之中。
合并:将两个集合合并为一个。
并查集的初始化伪代码

查找
通俗地讲一个故事:几个家族进行宴会,但是家族普遍长寿,所以人数众多。由于长时间的分离以及年龄的增长,这些人逐渐忘掉了自己的亲人,只记得自己的爸爸是谁了,而最长者(称为「祖先」)的父亲已经去世,他只知道自己是祖先。为了确定自己是哪个家族,他们想出了一个办法,只要问自己的爸爸是不是祖先,一层一层的向上问,直到问到祖先。如果要判断两人是否在同一家族,只要看两人的祖先是不是同一人就可以了。
在这样的思想下,并查集的查找算法诞生了。
如下图,要查找绿色节点的祖先节点,就需要先找出绿色节点的父亲节点,如果他的父亲节点不是祖先节点,那就接着找父亲节点的父亲节点,知道找出祖先节点为止。

查找函数的伪代码

路径压缩
这样一层一层地查找的确可以达成目的,但是显然效率实在太低。因为使用了大量没用的信息,一个节点的祖先是谁与他的父亲是谁没什么关系,这样一层一层找太浪费时间,不如直接让这个节点当祖先的儿子,问一次就可以出结果了。甚至祖先是谁都无所谓,只要这个人可以代表我们家族就能得到想要的效果。
把在路径上的每个节点都直接连接到根上,这就是路径压缩。
如下图,原本要查找绿色节点的祖先需要向上查询3次,而在查询过程中将查询路径上的节点的父亲节点都设置为祖先节点,在此查询时就只需要查询一次,效率明显提高了。

路径压缩的伪代码

时间复杂度:使用了路径压缩的并查集查询时间复杂度仅为$O(1)$
合并
宴会上,一个家族的祖先突然对另一个家族说:我们两个家族交情这么好,不如合成一家好了。另一个家族也欣然接受了。
上文说过,祖先是谁并不重要,所以只要其中一个祖先变成另一个祖先的父亲节点就可以了。
如下左图,将右边集合的祖先节点设置为左边集合的祖先节点的父亲节点,两个集合就合并成为一个集合。而右图将左边集合的祖先节点设置为右边集合的祖先节点的父亲节点,两个集合也是合并成为一个集合。


合并操作的伪代码

按秩合并
合并后可能会导致集合树的不平衡,增大树的深度,从而增加查询的耗时。一个控制树的深度的办法是,在合并时,比较两棵树的大小,较大的一棵树的根节点成为合并后的树的根节点,较小的一棵树的根节点则成为前者的子节点。
判断树的大小有两种常用的方法,一个是以树中元素的数量作为树的大小,这被称为按大小合并。伪代码如下:

需要注意的是,上面的代码中,只有根节点的size有意义,非根节点的size是没有意义的。
另一种做法则是使用“秩”来比较树的大小。“秩”的定义如下:
- 只有根节点的树(即只有一个元素的集合),秩为0;
- 当两棵秩不同的树合并后,新的树的秩为原来两棵树的秩的较大者;
- 当两棵秩相同的树合并后,新的树的秩为原来的树的秩加一。
在没有路径压缩优化时,树的秩等于树的深度减一。在有路径压缩优化时,树的秩仍然能反映出树的深度和大小。在合并时根据两棵树的秩的大小,决定新的根节点,这被称作按秩合并。用伪代码表示如下:

同样,上面的代码中,只有根节点的rank有意义,非根节点的rank是没有意义的。
由伪代码分析可得,使用了路径压缩的单次Union操作时间复杂度可以近似地认为是$O(1)$。由《算法导论》一书中定理21.1的证明可知,一个有n个点的集合,每个点的祖先节点最多被更新$⌈log n⌉$ 次,最多需要执行$n – 1$ 次Union操作,因此Union操作总的时间复杂度为$O(nlogn)$
并查集求桥
1)算法描述:对于给定的图,先将图中各个顶点初始化为属于各自顶点的集合,然后依次输入图的边,如果边对应的两个顶点属于不同的集合,则将这两个点进行合并,如果两点属于同一个集合则不进行操作,依次对所有的边操作完,计算图中共有几个祖宗节点,有几个祖宗节点就有几个连通块。记录下这个连通块的数量,然后生成一个生成树,初始化各点所属的集合,删除其中一条生成树的树边,按照其他边对应的两个点的关系合并集合,合并完成之后计算连通块的数量,如果连通块的数量比删除边之前的连通块数量多,那么删除的边就是桥。依次枚举完所有的树边,就可以找出所有的桥。**
2)伪代码描述:

3)算法时间复杂度:每次查询一条边的两个点所属集合的时间复杂度为$O(1)$,合并两个点所在的集合的时间复杂度为$O(1)$,共有m 条边,查询这些边对应的点所属集合的时间复杂度为$O(m)$。生成树的树边共有 $n – 1$ 条树边,初始化集合并删去其中一条树边后重新合并这些点,需要重复 $n – 1$ 次,算法总体的时间复杂度为$O(n m)$。
边双连通分量
在一张连通的无向图中,对于两个点 u 和 v,如果无论删去哪条边(只能删去一条)都不能使它们不连通,我们就说 u和v 边双连通。
若一个无向图中的去掉任意一条边都不会改变此图的连通性,即不存在桥,则称作边双连通图,边双连通图的任意一条边都至少在一个简单环中。一个无向图中的每一个极大边双连通子图称作此无向图的边双连通分量。
如下图,对于图①,删除图中任意一条边,图①中各点依旧保持连通。而如果同时删去(0,3)和(0,1)这两条边,那么节点0和其他节点将不再连通,那么图①则称为边双连通图。
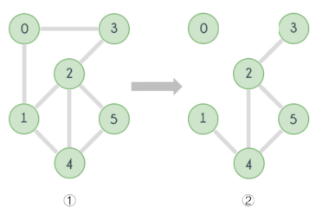
对于下图,只需要删除(0,3)这一条边(也就是桥),节点0就不再和其他节点连通,这样的图就不是边双连通图。图中节点2,4,5则构成了这个图的边双连通分量。
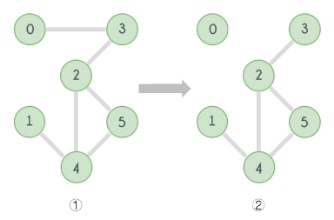
可以看出,桥将一个图中的边双连通分量划分开来。如果我们将每个边双连通分量都压缩成一个顶点,并且只将桥边作为边留在压缩后的图中,那么我们将得到一个无环图,即树。
如下图,将左图中的所有边双连通分量找出来之后进行压缩操作即可得到右图中的树。如果该图有多个连通分量,则得到森林。

当还没开始往图里添加边时时,它包含n个双连通的分量,这些分量之间本身是不连通的。(n为点数)
如右图,图中没有任何边,每个点都是一个双连通分量

每次往图中添加下一条边时,可能会出现三种情况:
1.边对应的两个点属于同一个双连通分量。
这条边会使得所在的双连通分量添加一条环边,不会改变森林的其他结构。在这种情况下,桥的数量不会发生变化。
如下图,桥的数量原本有编号的四条边,添加了黄色边之后,黄色边所在的双连通分量多了一条环边,而桥依旧是原本编号的四条边,并且没有发生连通分量或者双连通分量的合并。
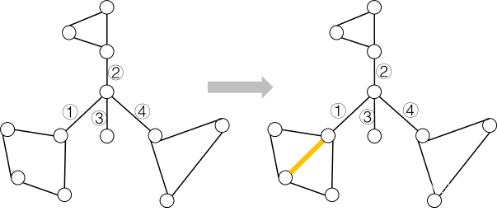
2.两点属于两个不同的连通分量
这条边对应的两个点原本属于两棵不同的树,加上这条边之后,会使的两个连通分量合并成一个,而这条边则成为连通这两个分量的唯一路径,也就是桥。在这种情况下,桥的数量加一,原有的旧桥依旧是桥,不受影响。
如下图,点①与点②原本属于两棵不同的树,连接点①和点②之后,他们所属的连通分量发生合并,现在他们都属于同一个连通分量,并且黄色边会成为新的桥,桥的数量加一。
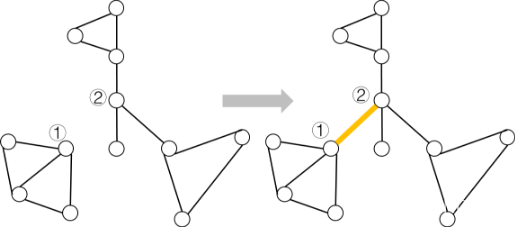
3.两点属于同一个连通分量,不同的双连通分量
在这种情况下,这条边与一些旧桥一起形成了环,由此产生的环需要被压缩成一个新的双连通分量。在这种情况下,新加入的边会被当作桥来处理,桥的数量会加一,紧接着把与这条边形成环的旧桥以及这条新桥给减掉,因此桥的数量会减少两条或者更多。
如下图,原本边(①,③)是一条桥,加入边(①,②)之后,桥(①,③)与边(①,②)形成环。先把边(①,②)当作桥处理,将桥的数量加一,然后把形成环的桥边(①,③)和(①,②)给去掉,这种情况下,桥的数量就减少了两条。
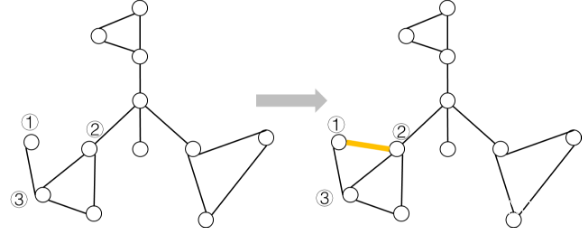
对于下图原本边(①,②),(①,③),(②,④)都是桥,加入边(③,④)之后,边(①,②),(①,③),(②,④)与(③,④)形成一个环,把(③,④)当作桥来处理,桥的数量加一,然后处理旧桥与这条新桥,在这种情况下,桥的数量减少四条。
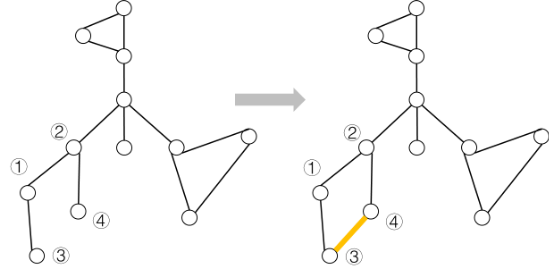
分析完上述三种情况后,我们可以发现求桥的数量可以被简化为维护图中双连通分量形成的森林以及这些双连通分量的有效压缩。
高效算法使用的数据结构
两个并查集,一个并查集用于维护图中的连通分量,另外一个并查集用于图中的双连通分量。同时两个并查集都采用路径压缩和按秩合并。
最小公共祖先
最小公共祖先简称 LCA(Lowest Common Ancestor)。两个节点的最小公共祖先,就是这两个点的公共祖先里面,离根最远的那个。
如下图,点1和点2的公共祖先节点有5,6,7,8,而离根节点最远的节点为5号点,点1和点2的最小公共祖先就是5号点。同理,3号点和4号点的LCA为6号点,2号点和5号点的LCA为5号点,因为5号点本身就是2号点的祖先节点。

压缩操作
在树中添加一条新的边(a,b),如果这条边对应的两点属于同一个连通分量,不同的双连通分量,那么就会形成一个新的环,a, b两点已经被(a,b)这条边连接,通过在树中寻找这两个点的LCA,我们就能找到这个新形成的环,这个环由边(a,b),a点在树上到LCA的路径,LCA到b点的路径这几个部分组成。
如下左图,在树中添加(①,②)这条边,①②⑤这三个点就会形成一个环,通过找到①,②两点的LCA 即⑤号点,我们就可以将他们在维护双连通分量的并查集中合并成一个集合。
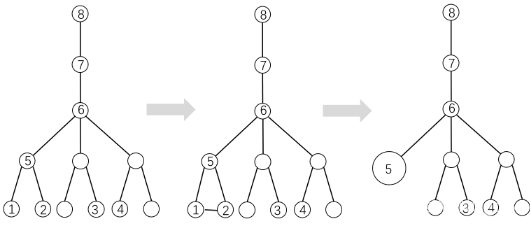
同理,⑤号所属集合中的一个点与⑦号点连一条线会与⑥号点形成一个新的环,通过⑦号点是这条新的边两点对应的LCA,⑤号点寻找LCA的路径为⑤ -> ⑥ -> ⑦,将五号点寻找LCA路径中经过的点合并到⑦号点所属的双连通分量集合中去。
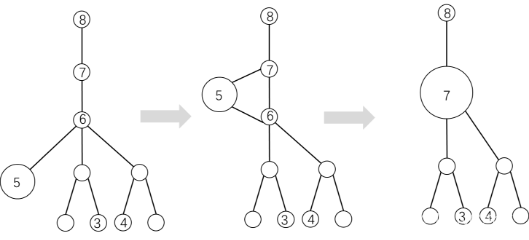
伪代码描述



算法时间复杂度
每次往图里添加一条新的边要查询两个点所属的连通分量集合及双连通分量的集合,一条边需要4次查询,共有m条边,一共需要查询$4 * m$ 次, 使用了路径压缩的并查集查询时间复杂度为$O(m)$。
每次合并集合的时间复杂度为$O(1)$,每个点的祖先节点最多被更新$⌈log n⌉$ 次,最多需要执行$n – 1$ 次合并操作,因此合并操作总的时间复杂度为$O(n log n)$。
算法整体的时间复杂度为$O(m + n log n)$。由于边数一般比点数多很多,因此整体复杂度主要取决于边数。
五、效率分析(时间单位:us)
注:下列表格中的DSU代表使用双连通分量压缩计算桥数量的算法
附件数据集的运行时间:
| 算法 | 中图 | 大图 |
|---|---|---|
| DSU | 77.9us | 0.2944s |
| Tarjan | 7.9us | 0.7173s |
| 桥的数量 | 0 | 8 |
在规模较小时,DSU算法的运行时间要大于Tarjan算法的运行时间,而当数据规模较大时,由于Tarjan算法的具体代码实现采用了递归的实现方式,会增加与算法效率本身无关的开销,所以运行时间要大于DSU算法的运行时间
O(m)复杂度时间理论值推导
$t_1 = m_1 * t$, t1表示规模为m1的数据用时
$t_2 = m_2 * t$, t2表示规模为m2的数据用时
$t2=(m2/m1) * t1$
O(n log(n))复杂度时间推导
$t_1=n_1*log(2,n_1)*t$, t1表示规模为n1的数据用时
$t_2=n_2*log(2,n_2)*t$, t2表示规模为n2的数据用时
$t_2=n_2/n_1*(log(2,n_2)/1og(2,n_1))* t_1$
基准法1 + 生成树优化随机数据测试
边数固定,点数从一千个点增加到五千个点
| 算法 | 点数 | 边数 | 基准法(us) | O(nm)参考值(us) |
|---|---|---|---|---|
| BaseTree | 1000 | 50000 | 3.15E+06 | 3.28E+06 |
| BaseTree | 2000 | 50000 | 6.79E+06 | 6.56E+06 |
| BaseTree | 3000 | 50000 | 1.02E+07 | 9.84E+06 |
| BaseTree | 4000 | 50000 | 1.33E+07 | 1.31E+07 |
| BaseTree | 5000 | 50000 | 1.64E+07 | 1.64E+07 |
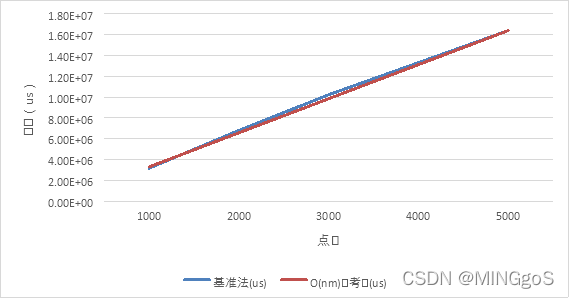
由上图可以看出,当点数远少于边数的时候基准法使用生成树优化的时间复杂度$O(m n + n^2)$中的$n^2$ 一项可以忽略不计,实际运行时间和参考值的曲线基本贴合在一起,拟合程度较好。
边数和点数相等,从一万个点到五万个点
| 算法 | 点数 | 边数 | 基准法(us) | O(n * n)参考值(us) |
|---|---|---|---|---|
| BaseTree | 10000.00 | 10000.00 | 2286580.00 | 2304804.00 |
| BaseTree | 20000.00 | 20000.00 | 10493700.00 | 9219216.00 |
| BaseTree | 30000.00 | 30000.00 | 22397300.00 | 20743236.00 |
| BaseTree | 40000.00 | 40000.00 | 38891000.00 | 36876864.00 |
| BaseTree | 50000.00 | 50000.00 | 57620100.00 | 57620100.00 |
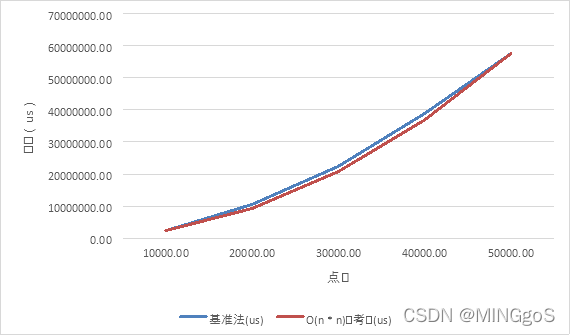
由上图可以看出,当点数和边数相接近时,算法的时间复杂度 $O(m n + n^2)$中的$m n$相当于$n^2$使得算法整体的时间复杂符合$O(n^2)$的增长趋势,实际运行时间和$O(n^2)$的曲线相接近,拟合程度较好。
DSU算法随机数据测试
点数固定,边数从两百万增加到一千二百万
时间单位:us
| 点数 | 边数 | DSU处理(us) | DSU理论值(us) | Tarjan |
|---|---|---|---|---|
| 5000 | 5000 | 569.3666667 | 24.11381667 | 311.5667 |
| 5000 | 2000000 | 11284.18 | 9645.526667 | 48975.98 |
| 5000 | 4000000 | 20081.04 | 19291.05333 | 98991.43 |
| 5000 | 6000000 | 30077.9 | 28936.58 | 150016.8 |
| 5000 | 8000000 | 39319.14 | 38582.10667 | 200799.7 |
| 5000 | 10000000 | 48158.5 | 48227.63333 | 254684.9 |
| 5000 | 12000000 | 57873.16 | 57873.16 | 302656.7 |
上表数据中理论值忽略了实际算法复杂$O(m + n log n)$中的$n log n$以一千两百万条边的处理时间作为基准值推导出其他数据规模的理论值,需要注意的是当边数和点数数量级接近时,$m$与 $n log n$的数量级相接近,算法实际运行时间受点数影响较大,所以五千个点,五千条边的实际处理时间和理论时间相差了二十多倍
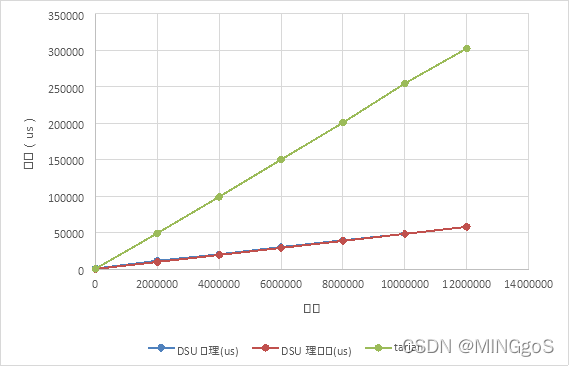
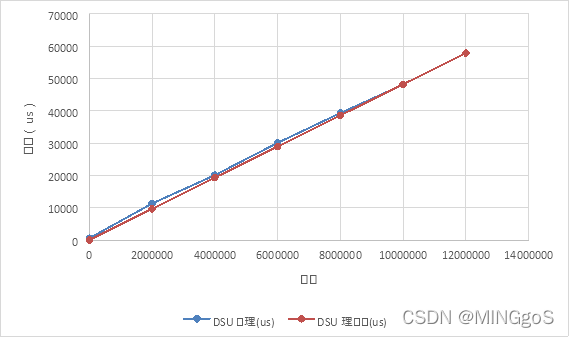
从图中可以看出当边数的数量远远大于点数时,理论值和实际值的拟合程度较高,算法的实际运行时间主要取决于边数。
稀疏图的算法效率分析
点数固定,边数增加:
十万个点的数据规模:
| 点数 | 边数 | DSU处理(us) | O(m)参考值(us) | O(nlogn)参考值 |
|---|---|---|---|---|
| 100000 | 100000 | 9466.95 | 9466.95 | 9466.95 |
| 100000 | 200000 | 10585.18 | 18933.9 | 20073.83 |
| 100000 | 300000 | 12031.1 | 28400.85 | 31110.98 |
| 100000 | 400000 | 11682.15 | 37867.8 | 42427.54 |
| 100000 | 500000 | 12317.5 | 47334.75 | 53951.86 |
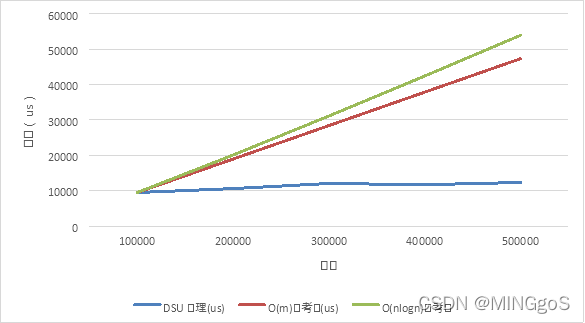
一百万个点的随机数据:
| 点数 | 边数 | DSU处理(us) | O(m)参考值(us) | O(n log n)参考值 |
|---|---|---|---|---|
| 1000000 | 1000000 | 15014 | 1.50E+04 | 15014.00 |
| 1000000 | 2000000 | 25135.1 | 3.00E+04 | 31534.55 |
| 1000000 | 3000000 | 27167.46667 | 4.50E+04 | 48623.75 |
| 1000000 | 4000000 | 30746 | 6.01E+04 | 66082.22 |
| 1000000 | 5000000 | 39939.8 | 7.51E+04 | 83815.28 |
| 1000000 | 6000000 | 50295 | 9.01E+04 | 101767.16 |
| 1000000 | 7000000 | 48344.23333 | 1.05E+05 | 119901.02 |
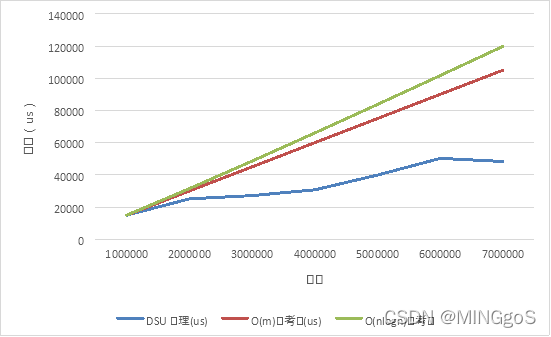
从上两张图中可以发现,当点数和边数相接近时,算法的实际运行时间和$O(m)$的参考值曲线拟合程度极差,说明当边数和点数相接近时,算法运行时间和边数关系不大。
还可以发现当边数提高到七百万条边时,与附件中的数据集规模相当,而算法的平均运行时间为四十多毫秒,而数据集中的文件需要接近三百毫秒的处理时间。可能的原因是附件中的数据集在算法运行中的合并次数比较多,最终数据集中的图只剩下一个连通分量,九个双连通分量,并且数据集中含有部分重边,跳过重边需要一部分时间,而随机图的生成是有进行去重的操作,所以花费的时间要远大于测试的随机数据平均值。
边数固定,点数增加:
| 点数 | 边数 | DSU处理(us) | O(n log n)参考值 |
|---|---|---|---|
| 100000 | 500000 | 12773.04 | 12773.04 |
| 200000 | 500000 | 13605.66 | 27084.11 |
| 300000 | 500000 | 13251.54 | 41975.69 |
| 400000 | 500000 | 13278.98 | 57244.27 |
| 500000 | 500000 | 13564.68 | 72793.17 |
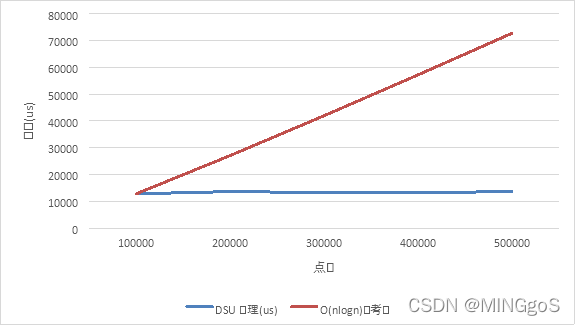
从上图可以发现,实际运行时间和$O(n log n)$的参考值并不拟合,事实上,只有在极端的情况下合并操作的时间复杂度才会达到 $O(n log n)$,在随机图数据测试中一般不会产生这种极端情况。
与Tarjan算法的效率对比:
稀疏图:边数 = 点数
时间单位:us
| 算法 | 点数 | 边数 | dsu | tar |
|---|---|---|---|---|
| DSU | 1000000 | 1000000 | 31327.22 | 52194.2 |
| DSU | 2000000 | 2000000 | 40378.46 | 93568.31667 |
| DSU | 3000000 | 3000000 | 48704.74 | 135942.35 |
| DSU | 4000000 | 4000000 | 56922.36 | 176652.6833 |
| DSU | 5000000 | 5000000 | 65829.04 | 210706.2667 |
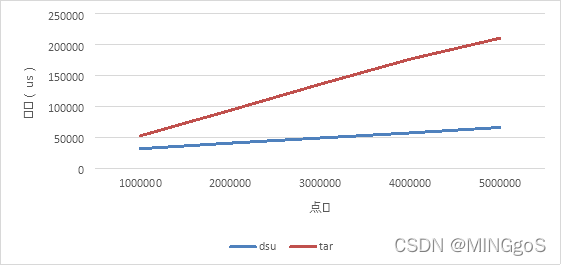
稠密图:$边数 = (点数 * 点数 ) / 2 * 0.96, m = n * n * 0.48$
| 算法 | 点数 | 边数 | 处理时间(us) | tarjan |
|---|---|---|---|---|
| DSU | 1000 | 480000 | 2571.66 | 8945.967 |
| DSU | 2000 | 1920000 | 9718.6 | 44108.47 |
| DSU | 3000 | 4320000 | 22239.98 | 106044 |
| DSU | 4000 | 7680000 | 37450.12 | 193829.9 |
| DSU | 5000 | 12000000 | 57873.16 | 356946.8 |
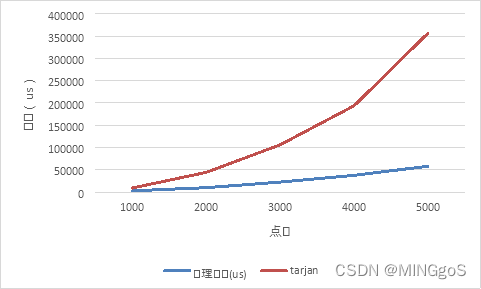
观察图表可得,DSU与Tarjan都为线性效率,但是tarjan的代码实现采用了递归的方式,无关的开销较多,实际运行时间要比DSU算法大
六、实验心得
-
在 Tarjan 的论文中,证明了不使用启发式合并、只使用路径压缩的最坏时间复杂度是$O(m log n)$。 在姚期智的论文中,证明了不使用启发式合并、只使用路径压缩,在平均情况下,时间复杂度依然是 $O(mα(m,n))$。由于路径压缩单次合并可能造成大量修改,有时路径压缩会破坏按秩合并的准确性,并不适合使用。在实际应用中,不一定总是需要两种优化一起使用。
-
有些人可能有一个误解,以为路径压缩优化后,并查集始终都是一个菊花图(只有两层的树的俗称)。但其实,由于路径压缩只在查询时进行,也只压缩一条路径,所以并查集最终的结构仍然可能是比较复杂的。
-
图算法的意义:图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物,连接两顶点的边则用于表示两个事物间具有这种关系